近日,九游平台(中国)数学与统计学院张洪侠老师在代数表示论领域的研究中取得了重要进展,相关成果分别与厦门大学数学科学学院陈健敏教授、阮诗佺副教授,以及日本大阪大学Takahashi Atsushi教授合作完成,并发表于代数学领域权威期刊《Journal of Algebra》。该期刊创刊于1964年,长期以来在代数学领域享有很高的学术声誉,是代数学领域的经典主流期刊,其学术影响力与学科贡献度广受国际认可。
一、关于加权射影直线上凝聚层范畴的几何模型研究
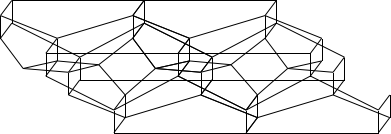
张洪侠老师与厦门大学陈健敏教授、阮诗佺副教授合作的研究,利用内边界上具有p个标记点、外边界上具有q个标记点的圆环面,建立了(p,q)型加权射影直线上凝聚层范畴的一种几何模型。在此模型框架下,建立了加权射影直线上不可分解层与标记圆环面中特定定向曲线同伦类之间的一一对应关系,并证明了不可分解层之间一次扩张群的维数等于对应曲线的正相交数。基于该几何模型,研究进一步刻画了凝聚层范畴的倾斜图与向量丛范畴的倾斜图的连通性,并对向量丛范畴的倾斜图给出了组合结构上的完整描述——该图或呈现为线性结构,或由四边形网格拼接构成。此外,论文证明了凝聚层范畴的自同构群同构于其对应的标记圆环面的映射类群,并揭示了两者分别作用于凝聚层范畴的倾斜图与几何模型三角剖分时的相容性。
二、关于导出范畴中完全例外序列及其轨道商结构的研究
张洪侠老师与日本大阪大学Atsushi Takahashi教授合作的研究,聚焦于tubular型加权射影直线上凝聚层范畴的有界导出范畴中的完全例外序列集合。重点探讨了该集合在球面扭转群作用下的轨道商结构及其性质,进而给出了该类轨道商个数的递推公式。该公式自然地推广了Dynkin情形及domestic型加权射影直线上凝聚层范畴的相应结果。此外,针对Legendre范式中单椭圆奇点通用展开所对应的Lyashko-Looijienga映射次数,本文给出了由Hertling与Roucairol所提出结果的一种新的表达形式,为该问题的研究提供了新的视角与工具。
论文地址:
1.https://doi.org/10.1016/j.jalgebra.2024.11.023
2.https://doi.org/10.1016/j.jalgebra.2024.12.021
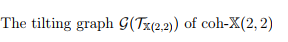
(数学与统计学院)
